Hằng đẳng thức cùng công thức lượng giác cơ bản sẽ theo suốt quá trình học tập môn Toán của học sinh từ cấp THCS cho đến đại học. Ôn lại 7 hằng đẳng thức đáng nhớ cùng công thức lượng giác qua các công thức tổng hợp dưới đây.
Table of Contents
7 hằng đẳng thức đáng nhớ và công thức mở rộng
1. Những hằng đẳng thức đáng nhớ
- Bình phương một tổng:
(a + b)2 = a2 + 2ab + b2
- Bình phương một hiệu:
(a – b)2 = a2 -2ab + b2
- Hiệu hai bình phương:
a2 – b2 = (a – b)(a + b)
- Lập phương một tổng:
(a + b)3 = a3 + 2a2b + 2ab2 + b3
- Lập phương một hiệu:
(a – b)3 = a3 – 2a2b + 2ab2 – b3
- Tổng hai lập phương:
a3 – b3 = (a + b)(a2 – ab + b2) = (a + b)3 – 3a2b – 3ab2 = (a + b)3 – 3ab(a – b)
- Hiệu hai lập phương:
a3 – b3 = (a – b)(a2 + ab + b2) = (a – b)3 + 3a2b – 3ab2 = (a – b)3 + 3ab(a – b)
2. Công thức mở rộng
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc
(a + b − c)2 = a2 + b2 + c2 + 2ab − 2ac − 2bc
(a – b − c)2 = a2 + b2 + c2 − 2ab − 2ac + 2bc
(a + b + c)3 = a3 + b3 + c3 + 3(a + b)(b + c)(c + a)
a3 + b3 + c3 − 3abc = (a + b + c)(a2 + b2 + c2 − ab − bc − ca)
(a – b)3 + (b – c)3 + (c – a)3 = 3(a – b)(b – c)(c – a)
(a + b)(b + c)(c + a) – 8abc = a(b – c)2 + b(c – a)2 + c(a – b)2
(a + b)(b + c)(c + a) = (a + b + c)(ab + bc + ca) − abc
(a + b)(b + c)(c + a) – 8abc = a(b – c)2 + b(c – a)2 + c(a – b)2
(a + b)(b + c)(c + a) = (a + b + c)(ab + bc + ca) − abc
3. Công thức tổng quát
an + bn = (a + b)(an−1 − an−2b + an−3b2 − an−4b3 +…+ a2bn−3 − abn−2 + bn−1)
an – bn = (a – b)(an–1 + an–2b + an–3b2 +…+ a2bn–3 + abn–2 + bn–1)
Với n ∈ N
MỘT SỐ HỆ QUẢ
Một số hệ quả với các hằng đẳng thức đáng nhớ dạng bậc 2:
Một số hệ quả với các hằng đẳng thức đáng nhớ dạng bậc 3:
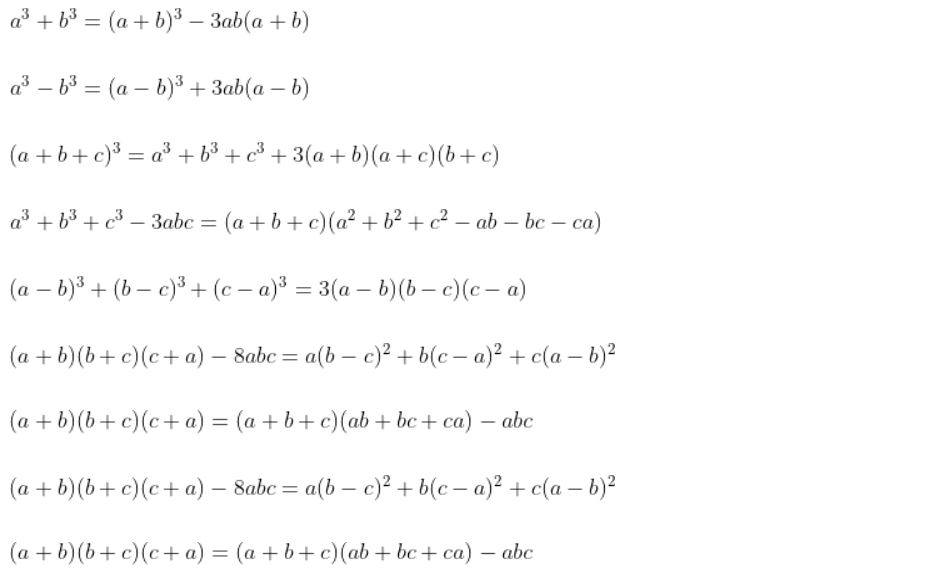
Một số hệ quả với các hằng đẳng thức đáng nhớ dạng tổng quát:
PHÁT BIỂU 7 HẰNG ĐẲNG THỨC ĐÁNG NHỚ BẰNG LỜI CỰC ĐƠN GIẢN
1, Bình phương của 1 tổng: Bình phương của 1 tổng sẽ (bằng =) bình phương của số thứ nhất (cộng +) với 2 lần tích của số thứ nhất nhân với số thứ hai và (cộng +) với bình phương của số thứ hai.
2, Bình phương của 1 hiệu: Bình phương của 1 hiệu sẽ (bằng =) bình phương của số thứ nhất (trừ –) đi 2 lần tích của số thứ nhất và số thứ hai sau đó (cộng +) bình phương với số thứ hai.
3, Hiệu hai bình phương: Hiệu hai bình phương của hai số sẽ (bằng =) tổng hai số đó (nhân x) với hiệu hai số đó.
4, Lập phương của 1 tổng: Lập phương của 1 tổng hai số sẽ (bằng =) lập phương của số thứ nhất (cộng +) với 3 lần tích bình phương số thứ nhất nhân số thứ hai, (cộng +) với 3 lần tích số thứ nhất nhân với bình phương số thứ hai, (cộng +) với lập phương số thứ hai.
5, Lập phương của 1 hiệu: Lập phương của 1 hiệu hai số sẽ (bằng =) lập phương của số thứ nhất (trừ –) đi 3 lần tích bình phương của số thứ nhất nhân với số thứ hai, (cộng +) với 3 lần tích số thứ nhất nhân với bình phương số thứ hai sau đó (trừ –) đi lập phương số thứ hai.
6, Tổng 2 lập phương: Tổng của hai lập phương hai số sẽ (bằng =) tổng của hai số đó (nhân x) với bình phương thiếu của hiệu hai số đó.
7, Hiệu 2 lập phương: Hiệu của hai lập phương của hai số sẽ (bằng =) hiệu hai số đó (nhân x) với bình phương thiếu của tổng của hai số đó.
MẸO GHI NHỚ HIỆU QUẢ

Theo anh Chu Cát Lượng (cựu học sinh của trường THCS – THPT Thạnh Thắng với giải ba cuộc thi HSG Toán THPT cấp tỉnh) chia sẻ rằng: “ Có không ít bạn học sinh cho rằng 7 hằng đẳng thức đáng nhớ thực sự rất “khó nhớ”. Theo mình thấy; một phần là do sự không thích học toán và một phần là do các bạn học sinh chưa làm nhiều các dạng bài tập liên quan.”
Thật vậy, để ghi nhớ hiệu quả nhất các hằng đẳng thức, các bạn hãy giải bài tập thật nhiều nhé! Ngoài ra, Studytienganh cũng sưu tầm một số tips nhỏ để bạn dễ học thuộc chúng hơn:
-
Nếu để ý kỹ, các bạn sẽ thấy hằng đẳng thức số 1 và 2, 4 và 5, 6 và 7 khá tương tự nhau và chúng chỉ khác nhau một chút về dấu. Vì thế, khi học hằng đẳng thức, thay vì học cả 7, chúng ta chỉ cần học 4 và lưu nhớ thêm dấu của nó.
-
Bên cạnh đó, các bạn có thể theo dõi bài hát “7 Hằng Đẳng Thức Đáng Nhớ” của “Nhật Anh sáng tạo” dựa trên nền nhạc của bài “Sau Tất Cả”. Với sự linh hoạt, mới mẻ trong cách học này sẽ giúp các bạn cảm thấy thư giãn hơn và học được tốt thấm nhuần kiến thức được tốt
Các dạng bài toán bảy hằng đẳng thức đáng nhớ
- Dạng 1: Tính giá trị của các biểu thức.
- Dạng 2: Chứng minh biểu thức A mà không phụ thuộc biến.
- Dạng 3: Áp dụng để tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức.
- Dạng 4: Chứng minh đẳng thức bằng nhau.
- Dạng 5: Chứng minh bất đẳng thức
- Dạng 6: Phân tích đa thức thành nhân tử.
- Dạng 7: Tìm giá trị của x
- Dạng 8: Thực hiện phép tính phân thức
- Dạng 9: Thực hiện phép tính phân thức
Dạng 1: Tính giá trị của biểu thức
Bài 1 :tính giá trị của biểu thức : A = x2 – 4x + 4 tại x = -1
Giải.
Ta có : A = x2 – 4x + 4 = A = x2 – 2.x.2 + 22 = (x – 2)2
Tại x = -1 : A = ((-1) – 2)2=(-3)2= 9
Vậy : A(-1) = 9
Dạng 2: Chứng minh biểu thức A không phụ thuộc vào biến
B = (x – 1)2 + (x + 1)(3 – x)
Giải.
B =(x – 1)2 + (x + 1)(3 – x)
= x2 – 2x + 1 – x2 + 3x + 3 – x
= 4 : hằng số không phụ thuộc vào biến x.
Dạng 3 : Tìm giá trị nhỏ nhất của biểu thức
C = x2 – 2x + 5
Giải.
Ta có : C = x2 – 2x + 5 = (x2 – 2x + 1) + 4 = (x – 1)2 + 4
Mà : (x – 1)2 ≥ 0 với mọi x.
Suy ra : (x – 1)2 + 4 ≥ 4 hay C ≥ 4
Dấu “=” xảy ra khi : x – 1 = 0 hay x = 1
Nên : Cmin= 4 khi x = 1
Dạng 4: Tìm giá trị lớn nhất của biểu thức
D = 4x – x2
Giải.
Ta có : D = 4x – x2 = 4 – 4 + 4x – x2 = 4 – (4 + x2 – 4x) = 4 – (x – 2)2
Mà : -(x – 2)2 ≤ 0 với mọi x.
Suy ra : 4 – (x – 2)2 ≤ 4 hay D ≤ 4
Dấu “=” xảy ra khi : x – 2 = 0 hay x = 2
Nên : Dmax= 4 khi x = 2.
Dạng 5: Chứng minh đẳng thức
(a + b)3 – (a – b)3 = 2b(3a2 + b2)
Giải.
VT = (a + b)3 – (a – b)3
= (a3 + 3a2b + 3ab2 + b3) – (a3 – 3a2b + 3ab2 – b3)
= a3 + 3a2b + 3ab2 + b3 – a3 + 3a2b – 3ab2 + b3
= 6a2b + 2b3
= 2b(3a2 + b2) ->đpcm.
Vậy : (a + b)3 – (a – b)3 = 2b(3a2 + b2)
Dạng 6: Chứng minh bất đẳng thức
Biến đổi bất đẳng thức về dạng biểu thức A ≥ 0 hoặc A ≤ 0. Sau đó dùng các phép biến đổi đưa A về 1 trong 7 hằng đẳng thức.
Dang 7: Phân tích đa thức thành nhân tử
F = x2 – 4x + 4 – y2
Giải.
Ta có : F = x2 – 4x + 4 – y2
= (x2 – 4x + 4) – y2 [nhóm hạng tử]
= (x – 2)2 – y2 [đẳng thức số 2]
= (x – 2 – y )( x – 2 + y) [đẳng thức số 3]
Vậy : F = (x – 2 – y )( x – 2 + y)
Bài 1: A = x3 – 4×2 + 4x
= x(x2 – 4x + 4)
= x(x2 – 2.2x + 22)
= x(x – 2)2
Bài 2: B = x 2 – 2xy – x + 2y
= (x 2– x) + (2y – 2xy)
= x(x – 1) – 2y(x – 1)
= (x – 1)(x – 2y)
Bài 3: C = x2 – 5x + 6
= x2 – 2x – 3x + 6
= x(x – 2) – 3(x – 2)
= (x – 2)(x – 3)
Dạng 8 : Tìm x. biết :
x2 ( x – 3 ) – 4x + 12 = 0
Giải.
x2 ( x – 3 ) – 4x + 12 = 0
x2 ( x – 3 ) – 4(x – 3 ) = 0
( x – 3 ) (x2 – 4) = 0
( x – 3 ) (x – 2)(x + 2) = 0
( x – 3 ) = 0 hay (x – 2) = 0 hay (x + 2) = 0
x = 3 hay x = 2 hay x = –2
vậy : x = 3; x = 2; x = –2
Dạng 9: Thực hiện phép tính phân thức
Tính giá trị của phân thức M = tại x = –1
Giải.
ta có : M =
=
Khi x = -1 : M =
Vậy : M = tại x = -1 .
Một số lưu ý về hằng đẳng thức đáng nhớ
Lưu ý: a và b có thể là dạng chữ (đơn phức hoặc đa phức) hay a,b là một biểu thức bất kỳ. Khi áp dụng các hằng đẳng thức đáng nhớ vào bài tập cụ thể thì điều kiện của a, b cần có để thực hiện làm bài tập dưới đây:
- Biến đổi các hằng đẳng thức chủ yếu là sự biến đổi từ tổng hay hiệu thành tích giữa các số, kỹ năng phân tích đa thức thành nhân tử cần phải thành thạo thì việc áp dụng các hằng đẳng thức mới có thể rõ ràng và chính xác được.
- Để có thể hiểu rõ hơn về bản chất của việc sử dụng hằng đẳng thức thì khi áp dụng vào các bài toán, bạn có thể chứng minh sự tồn tại của hằng đẳng thức là đúng đắn bằng cách chuyển đổi ngược lại và sử dụng các hằng đẳng thức liên quan đến việc chứng minh bài toán.
- Khi sử dụng hằng đẳng thức trong phân thức đại số, do tính chất mỗi bài toán bạn cần lưu ý rằng sẽ có nhiều hình thức biến dạng của công thức nhưng bản chất vẫn là những công thức ở trên, chỉ là sự biến đổi qua lại sao cho phù hợp trong việc tính toán.
Bài tập về hằng đẳng thức
1. Bài tập tự luyện
Bài 1: Tính
a) (x + 2y)2;
b) (x – 3y)(x + 3y);
c) (5 – x)2.
d) (x – 1)2;
e) (3 – y)2
f) (x – )2.
Bài 2: Viết các biểu thức sau dưới dạng bình phương một tổng
a) x2+ 6x + 9;
b) x2+ x + ;
c) 2xy2 + x2y4 + 1.
Bài 3: Rút gọn biểu thức
a) (x + y)2+ (x – y)2;
b) 2(x – y)(x + y) +(x – y)2+ (x + y)2;
Bài 4: Tìm x biết
a) (2x + 1)2- 4(x + 2)2= 9;
b) (x + 3)2 – (x – 4)( x + 8) = 1;
c) 3(x + 2)2+ (2x – 1)2- 7(x + 3)(x – 3) = 36;
Bài 5: Tính nhẩm các hằng đẳng thức sau
a) 192; 282; 812; 912;
b) 19. 21; 29. 31; 39. 41;
c) 292- 82; 562- 462; 672 – 562;
Bài 6: Chứng minh rằng các biểu thức sau luôn dương với mọi giá trị của biến x
a) 9×2- 6x +2;
b) x2 + x + 1;
c) 2×2 + 2x + 1.
Bài 7: Tìm giá trị nhỏ nhất của các biểu thức
a) A = x2- 3x + 5;
b) B = (2x -1)2+ (x + 2)2;
Bài 8: Tìm giá trị lớn nhất của các biểu thức
a) A = 4 – x2 + 2x;
b) B = 4x – x2;
Bài 9: Tính giá trị của biểu thức
A. x3+ 12×2+ 48x + 64 tại x = 6
B = x3 – 6×2 + 12x – 8 tại x = 22
C= x3+ 9×2+ 27x + 27 tại x= – 103
D = x3 – 15×2 + 75x – 125 tại x = 25
Bài 10.Tìm x biết:
a) (x – 3)(x2+ 3x + 9) + x(x + 2)(2 – x) = 1;
b) (x + 1)3- (x – 1)3 – 6(x – 1)2 = -10
Bài 11: Rút gọn
| a. (x – 2)3 – x(x + 1)(x – 1) + 6x(x – 3)
b. (x – 2)(x2 – 2x + 4)(x + 2)(x2 + 2x +4) |
d. (x + y)3 – (x – y)3 – 2y3
e. (x + y + z)2 – 2(x + y + z)(x + y) + (x + y) |
e. (2x + y)(4×2– 2xy +y2) – (2x – y)(4×2+ 2xy + y2)
Bài 12: Chứng minh
a. a3+ b3 = (a + b)3– 3ab(a + b)
b. a3 – b3 = (a – b)3 – 3ab(a – b)
Bài 13: a. Cho x + y = 1. Tính giá trị của biểu thức x3 + y3 + 3xy
Cho x – y = 1. Tính giá trị của biểu thức x3- y3- 3xy
Bài 14: Chứng minh biểu thức sau không phụ thuộc vào x:
A = (2x + 3)(4×2– 6x + 9) – 2(4×3– 1)
B = (x + y)(x2– xy + y2) + (x – y)(x2+ xy + y2) – 2×3.
Bài 15. Cho a + b + c = 0. Chứng minh M= N= P với
M = a(a + b)(a + c); N = b(b + c)(b + a); P = c(c + a)(c + b);
2. Bài tập nâng cao
Bài 1. Cho đa thức 2x² – 5x + 3 . Viết đa thức trên dưới dạng 1 đa thức của biến y trong đó y = x + 1.
Lời Giải
Theo đề bài ta có: y = x + 1 => x = y – 1.
A = 2x² – 5x + 3
= 2(y – 1)² – 5(y – 1) + 3 = 2(y² – 2y + 1) – 5y + 5 + 3 = 2y² – 9y + 10
Bài 2. Tính nhanh kết quả các biểu thức sau:
a) 127² + 146.127 + 73²
b) 98.28– (184 – 1)(184 + 1)
c) 100² – 99² + 98² – 97² + …+ 2² – 1²
d) (20² + 18² + 16² +…+ 4² + 2²) – ( 19² + 17² + 15² +…+ 3² + 1²)
Lời Giải
a) A = 127² + 146.127 + 73²
= 127² + 2.73.127 + 73²
= (127 + 73)²
= 200²
= 40000 .
b) B = 9 8 .2 8 – (18 4 – 1)(18 4 + 1)
= 188 – (188 – 1)
= 1
c) C = 100² – 99² + 98² – 97² + …+ 2² – 1²
= (100 + 99)(100 – 99) + (98 + 97)(98 – 97) +…+ (2 + 1)(2 – 1)
= 100 + 99 + 98 + 97 +…+ 2 + 1
= 5050.
d) D = (20² + 18² + 16² +…+ 4² + 2²) – ( 19² + 17² + 15² +…+ 3² + 1²)
= (20² – 19²) + (18² – 17²) + (16² – 15²)+ …+ (4² – 3²) + (2² – 1²)
= (20 + 19)(20 – 19) + (18 + 17)(18 – 17) + ( 16 +15)(16 – 15)+ …+ (4 + 3)(4 – 3) + (2 + 1)(2 – 1)
= 20 + 19 + 18 + 17 + 16 +15 + …+ 4 + 3 + 2 + 1
= 210
Bài 3. So sánh hai số sau, số nào lớn hơn?
a) A = (2 + 1)(22+ 1)(24+ 1)(28 + 1)(216 + 1) và B = 232
b) A = 1989.1991 và B = 19902
Gợi ý đáp án
a) Ta nhân 2 vế của A với 2 – 1, ta được:
A = (2 – 1)(2 + 1)(22 + 1)(24 + 1)(28 + 1)(216 + 1)
Ta áp dụng đẳng thức ( a- b)(a + b) = a² – b² nhiều lần, ta được:
A = 232 – 1.
=> Vậy A < B.
b) Ta đặt 1990 = x => B = x²
Vậy A = (x – 1)(x + 1) = x² – 1
=> B > A là 1.
Bài 4. Chứng minh rằng:
a) a(a – 6) + 10 > 0.
b) (x – 3)(x – 5) + 4 > 0.
c) a² + a + 1 > 0.
Lời Giải
a) VT = a² – 6a + 10 = (a – 3)² + 1 ≥ 1
=> VT > 0
b) VT = x² – 8x + 19 = (x – 4)² + 3 ≥ 3
=> VT > 0
c) a² + a + 1 = a² + 2.a.½ + ¼ + ¾ = (a + ½ )² + ¾ ≥ ¾ >0.
