Z hay tập hợp Z trong số học là gì? Đây là một câu hỏi được khá nhiều bạn học sinh đưa ra khi giải các bài tập toán đặc biệt là trong chương trình toán lớp 6. Nhưng không phải ai cũng có thể dễ dàng đưa ra một câu trả lời chính xác và đầy đủ về nó. Vậy hôm nay chúng ta hãy cùng nhau tìm hiểu kĩ hơn về kí hiệu Z trong số học là gì? cũng như những vấn đề liên quan nhé.
Table of Contents
Tập hợp Z trong số học là gì?
Cùng tìm hiểu kiến thức về các tập hơp Z qua phần sau nhé.
Giới thiệu về Tập hợp Z
Tập hợp Z hay còn gọi với tên khác là tập hợp các số nguyên, bao gồm: các số nguyên âm, số 0 và các số nguyên dương.

Trong đó:
- Số nguyên dương là tất cả các số tự nhiên khác 0. Ví dụ: +1; +2; +3; … hoặc có thể bỏ đi dấu “+” và ghi là: 1; 2; 3; 4; …
- Số nguyên âm là các số -1; -2; -3; 4; ….
- Số 0 không phải là số nguyên âm và cũng không phải là số nguyên dương
Kí hiệu: tập hợp các số nguyên thường được biểu thị bằng chữ in đậm (Z) với chữ cái “Z” bắt nguồn từ tiếng Đức Zahlen (nghĩa là “số”)
Như vậy, ta có tập hợp các số nguyên: Z= {….; -3; -2; -1; 0; 1; 2; 3; ….}
Tập hợp Z+ và Z- là gì?
Như chúng ta đã tìm hiểu ở phần trước, ngoại trừ số 0 thì tập hợp các số nguyên Z sẽ bao gồm các số nguyên dương và các số nguyên âm. Sự phân chia này không chỉ giúp chúng ta dễ phân biệt về mặt hình thức mà còn có ý nghĩa đại số, góp phần to lớn cho các công trình số học sau này.
Ta có:
- Z+ là ký hiệu cho số nguyên dương.
- Z- là ký hiệu cho số nguyên âm.
Đây là những ký hiệu không chính thống do mỗi quốc gia, mỗi nền giáo dục khác nhau quy định và tại Việt Nam chúng ta quy ước như trên.
Ví dụ:
- Tập hợp Z+ là: 1; 2; 3; 4; 5; ….
- Tập hợp Z- là: -1; -2; -3; -4; -5; ….
Mối liên hệ giữa các tập hợp số trong toán học
Trong toán học, chúng ta sẽ thường bắt gặp 5 tập hợp số chính:
- Tập N các số tự nhiên
- Tập Z các số nguyên
- Tập Q các số hữu tỉ
- Tập I các số vô tỉ
- Tập R các số thực
Khi đó quan hệ bao hàm giữa các tập hợp số trong toán học là: N ⊂ Z ⊂ Q ⊂ R
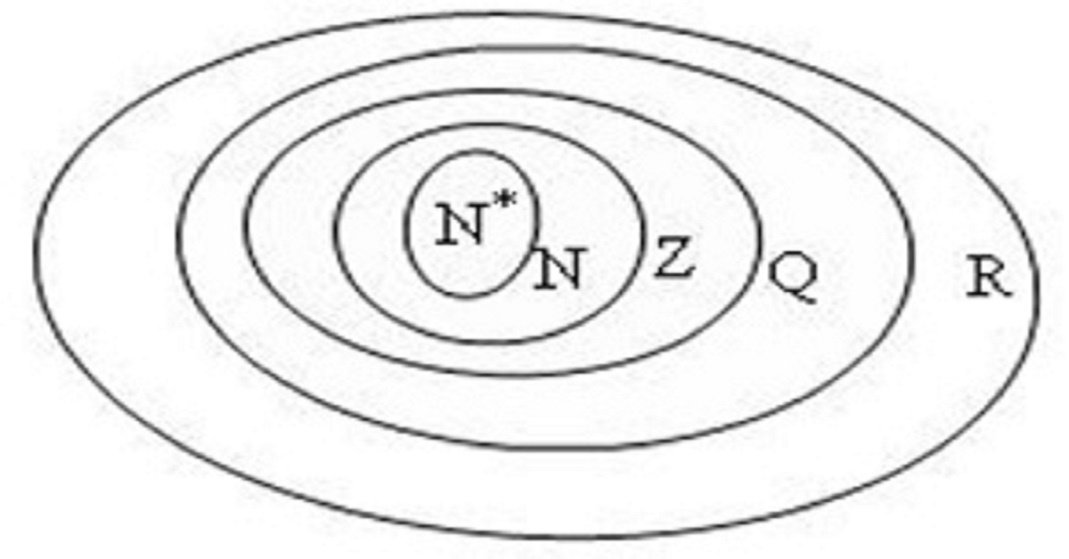
Và giống như tập hợp các số tự nhiên N, “Z là tập hợp vô hạn đếm được.”
Biểu diễn số nguyên Z trên trục số
Vậy tập hợp Z được biểu diễn như thế nào? Các bước thực hành ra sao?
Cách biểu diễn Z trên trục
Người ta biểu diễn các số nguyên Z trên trục số nằm ngang hoặc nằm dọc như hình dưới đây:
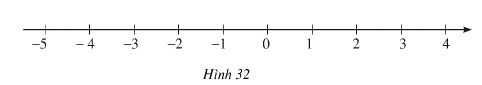
- Hình biểu diễn các số nguyên gọi là trục số.
- Điểm 0 (không) được quy ước là điểm gốc của trục số.
- Chiều nhìn từ phải sang trái tính từ điểm gốc của trục số (điểm 0) gọi là chiều âm, chiều nhìn từ trái sang phải tính từ điểm 0 gọi là chiều dương của trục số.
- Điểm biểu diễn số nguyên a trên trục số (nằm ngang hoặc nằm dọc) được gọi là điểm a.
Các bước biểu diễn Z chi tiết
Sau đây sẽ là các bước để giúp các bạn có thể dễ dàng biểu diễn các số nguyên trên trục số nằm ngang một cách chính xác và nhanh nhất:
- Bước 1: Kẻ một mũi tên nằm ngang có chiều từ trái sang phải (còn gọi là chiều dương).
- Bước 2: Vạch trên mũi tên vừa vẽ các điểm cách đều nhau. (Mỗi điểm này là một số nguyên, điểm biểu diễn cho số nguyên a được gọi là điểm a. Khoảng cách giữa hai số gần nhau nhất được gọi là 1 đơn vị.)
- Bước 3: Xác định một điểm (nằm ở khoảng giữa) làm điểm gốc của trục số (hay còn gọi là điểm 0).
- Bước 4: Từ điểm 0 viết lần lượt về phía bên trái (chiều âm) các số nguyên âm: -1; -2; -3; -4; …
- Bước 5: Từ điểm 0 viết lần lượt về phía bên phải (chiều dương) các số nguyên dương: 1; 2; 3; 4; …
Như vậy, việc biểu diễn số nguyên trên trục số không chỉ giúp chúng ta có thể sắp xếp các số nguyên trong một tập hợp mà còn để so sánh các số nguyên với nhau trong phần tiếp theo.
So sánh hai số nguyên Z
Khi muốn so sánh hai số nguyên với nhau, chúng ta có thể vận dụng những kiến thức đã được học trong phần biểu diễn các số nguyên trên trục số. Từ đó, ta có kết luận như sau:
Khi biểu diễn hai số nguyên b,c trên trục số nằm ngang, nếu điểm b nằm bên trái điểm c thì ta nói b nhỏ hơn c hoặc c lớn hơn b và ghi là: b < c hoặc c > b.
Ví dụ:
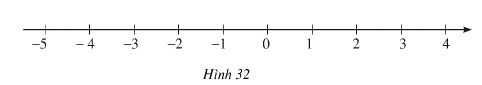
Số -4 nằm bên phải số -5 vậy ta nói -4 lớn hơn -5 và ghi được là -4 > -5, hoặc ta nói -5 nhỏ hơn -4 và ghi được là -5 < -4.
Từ ví dụ trên, có một số lưu ý chúng ta cần phải lưu ý như sau:
- Tất cả số nguyên dương (1; 2; 3; …) đều lớn hơn số 0.
- Tất cả số nguyên âm (-1; -2; -3; …) đều nhỏ hơn số 0.
- Tất cả số nguyên âm đều nhỏ hơn bất kỳ số nguyên dương nào.
- Khi so sánh hai số nguyên âm, số đối của số nào nhỏ hơn thì số đó lớn hơn.
Thứ tự trong tập hợp các số nguyên Z
Các bài tập liên quan đến phần này thường sẽ yêu cầu chúng ta sắp xếp các số nguyên theo thứ tự tăng dần hoặc thứ tự giảm dần. Vì vậy, để có thể hoàn thành tốt các dạng bài tập này, các bạn cần áp dụng việc so sánh các số nguyên với nhau trong một tập hợp để không bị bỏ sót và cho ra được đáp án đúng.
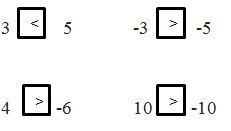
Để dễ hình dung hơn, chúng ta cùng đến với một ví dụ sau:
Sắp xếp các số -9; 5; -3; 0; 2 theo thứ tự tăng dần
Nhìn vào tập hợp số nguyên trên ta thấy: -9 < -3 < 0 < 2 < 5. Vậy, ta được dãy số mới sắp xếp theo thứ tự tăng dần là: -9; -3; 0; 2; 5
Trên đây là những kiến thức cơ bản giúp các bạn giải đáp thắc mắc cho câu hỏi Z trong số học là gì? Hy vọng rằng bài viết có thể đem đến được cho các bạn cái nhìn tổng quát về tập hợp Z trong toán học để từ đó giải được các dạng bài tập liên quan. Nếu có bất kỳ thắc mắc hay lời nhận xét nào về bài viết, các bạn hãy để lại bình luận ở phía dưới, chúng tôi sẽ cố gắng giải đáp trong thời gian sớm nhất. Chúc các bạn đạt hoàn thành tốt các bài tập được giao nhé.