Công thức lượng giác cơ bản chương trình học THCS & THPT

Công thức lượng giác cơ bản, công thức nâng cao, công thức nghiệm được tóm tắt đầy đủ, dễ nhớ mà chúng ta phải thường xuyên sử dụng để giải bài tập.

Công thức lượng giác cơ bản

1. Các cung đặc biệt.

Hai cung đối nhau: α và – α

  • cos (-x) = cos x
  • sin (-x) = -sin x
  • tan (-x) = -tan x
  • cot (-x) = -cot x

Hai cung bù nhau: α và π – α

  • sin (π – x) = sin x
  • cos (π – x) = -cos x
  • tan (π – x) = -tan x
  • cot (π – x) = -cot x

Hai cung phụ nhau: α và π/2 – α

  • sin (π/2 – x) = cos x
  • cos (π/2 – x) = sin x
  • tan (π/2 – x) = cot x
  • cot (π/2 – x) = tan x

Hai cung hơn kém π

  • sin (π + x) = -sin x
  • cos (π + x) = -cos x
  • tan (π + x) = tan x
  • cot (π + x) = cot x

Hai cung hơn kém nhau π/2

  • sin (π/2 + x) = cos x
  • cos (π/2 + x) = -sin x
  • tan (π/2 + x) = -cot x
  • cot (π/2 + x) = -tan x

2. Các công thức lượng giác căn bản.

1.\ \tan x=\frac{\sin x}{\cos x}

2.\ \cot x=\frac{\cos x}{\sin x}

3.\ \sin^2x+\cos^2x=1

4.\ \tan x.\cot x=1\left(x\ne k\frac{\pi}{2},\ k\ ∈\ Z\right)

5.\ 1+\tan^2x=\frac{1}{\cos^2x}\ \left(x\ne\frac{\pi}{2}+k\pi,\ k\ ∈\ Z\right)

6.\ 1+\cot^2x=\frac{1}{\sin^2x}\ \left(x\ne k\pi,\ k\ ∈\ Z\right)

1. sin (a ± b) = sin a.cos b ± cos a.sin b

2. cos (a + b) = cos a.cos b – sin a.sin b

3. cos (a – b) = cos a.cos b + sin a.sin b

4.\ \tan\left(a+b\right)=\frac{\tan a+\tan b}{1-\tan.\tan b}

5.\ \tan\left(a-b\right)=\frac{\tan a-\tan b}{1+\tan a.\tan b}

Mẹo nhớ công thức cộng: Sin thì sin cos cos sin, cos thì cos cos sin sin dấu trừ. Tan thì tan nọ tan kia chia cho mẫu số 1 trừ tan tan.

3. Công thức cộng

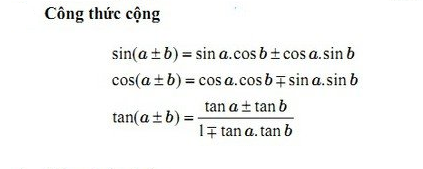
4. Công thức nhân đôi

  • sin2a = 2sina.cosa
  • cos2a = cos2a – sin2a = 2cos2a – 1 = 1 – 2sin2a
  • \tan2a=\frac{2\tan a}{1-\tan^2a}
  • \cot2a=\frac{\cot^2a\ -1}{2\cot a}

5. Công thức nhân ba

  • sin3a = 3sina – 4sin3a
  • cos3a = 4cos3a – 3cosa
  • \tan3a=\frac{3\tan a-\tan^3a}{1-3\tan^2a}
  • \cot3a=\frac{\cot^3a-3\cot a}{3\cot^2a-1}

6. Công thức nhân bốn:

  • sin4a = 4.sina.cos3a – 4.cosa.sin3a
  • cos4a = 8.cos4a – 8.cos2a + 1
  • hoặc cos4a = 8.sin4a – 8.sin2a + 1

7. Công thức hạ bậc

Thực ra những công thức này đều được biến đổi ra từ công thức lượng giác cơ bản, ví dụ như: sin2a=1 – cos2a = 1 – (cos2a + 1)/2 = (1 – cos2a)/2.

1.\ \sin^2a\ =\ \frac{1-\cos2a}{2}

2.\ \cos^2a=\frac{1+\cos2a}{2}

3.\ \sin^3a=\frac{3\sin a-\sin3a}{4}

4.\ \cos^3a=\frac{3\cos a+\cos3a}{4}

8. Công thức đổi biến đổi tích thành tổng

1.\ \cos a.\cos b=\frac{1}{2}\left[\cos\left(a+b\right)+\cos\left(a-b\right)\right]2.\ \sin a.\sin b=-\frac{1}{2}\left[\cos\left(a+b\right)-\cos\left(a-b\right)\right]

3.\ \sin a.\cos b=-\frac{1}{2}\left[\sin\left(a+b\right)+\sin\left(a-b\right)\right]

9. Công thức đổi biến đổi tổng thành tích

Mẹo nhớ: cos cộng cos bằng 2 cos cos, cos trừ cos bằng trừ 2 sin sin; sin cộng sin bằng 2 sin cos, sin trừ sin bằng 2 cos sin.

1.\ \cos a+\cos b=2\cos\frac{a+b}{2}.\cos\frac{a-b}{2}

2.\ \cos a-\cos b=-2\sin\frac{a+b}{2}.\sin\frac{a-b}{2}

3.\ \sin\ a+\sin b=2\sin\frac{a+b}{2}.\cos\frac{a-b}{2}

4.\ \sin\ a-\sin b=2\cos\frac{a+b}{2}.\sin\frac{a-b}{2}

5.\ \tan a+\tan b=\frac{\sin\left(a+b\right)}{\cos a.\cos b}

6.\ \tan a-\tan b=\frac{\sin\left(a-b\right)}{\cos a.\cos b}

7.\ \sin a+\cos a=\sqrt{2}\sin\left(a+\frac{\pi}{4}\right)=\sqrt{2}\cos\left(a-\frac{\pi}{4}\right)

8.\ \sin a-\cos a=\sqrt{2}\sin\left(x-\frac{\pi}{4}\right)=-\sqrt{2}\cos\left(x+\frac{\pi}{4}\right)

9.\ \tan a+\cot a=\frac{2}{\sin2a}

10.\ \cot a-\tan a=2\cot2a

11.\ \sin^4a+\cos^4a=1-\frac{1}{2}\sin^22a=\frac{1}{4}\cos4a+\frac{3}{4}

12.\ \sin^6a+\cos^6a=1-\frac{3}{4}\sin^22a=\frac{3}{8}\cos4a+\frac{5}{8}

9. Dấu của các giá trị lượng giác

Góc phần tư số I II III IV
Giá trị lượng giác
sin x + + – –
cos x + – – +
tan x + – + –
cot x + – + –

10. Bảng giá trị lượng giác một số góc đặc biệt

Bảng giá trị lượng giác một số góc đặc biệt

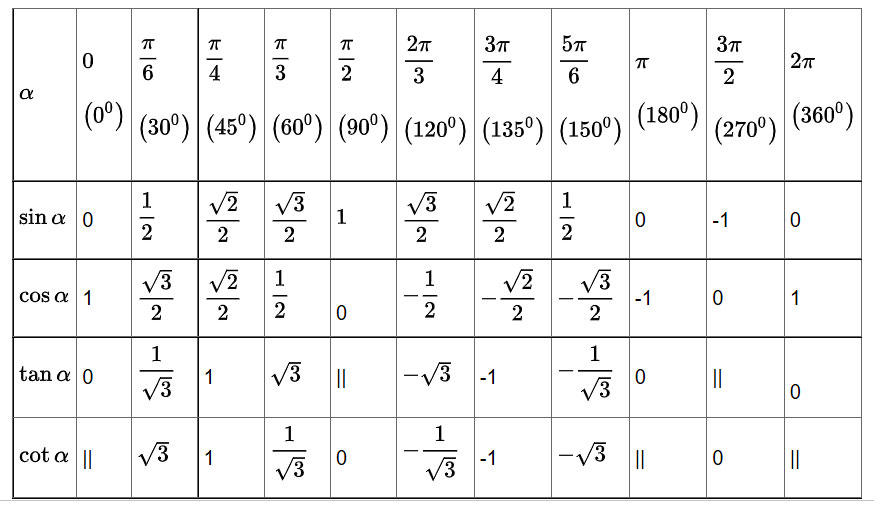
11. Công thức lượng giác bổ sung

Biểu diễn công thức theo t=\frac{\tan a}{2}

1.\ \sin a=\frac{2t}{1+t^2}\ \ \ \ \ \ \ \ \ \ \ \ 2.\ \cos a=\frac{1-t^2}{1+t^2}

3.\ \tan\ a=\frac{2t}{1-t^2}\ \ \ \ \ \ \ \ \ \ 4.\ \cot a=\frac{1-t^2}{2t}

  • Các công thức đạo hàm và đạo hàm lượng giác đầy đủ

Phía trên đây là tổng hợp các công thức lượng giác cơ bản dành cho học sinh trung học phổ thông. Nắm được những công thức trên có thể giúp chúng ta thực hiện tốt các bài tập rút gọn, chứng minh biểu thức, giải phương trình lượng giác. Vận dụng khéo léo những công thức trên thì quá trình học chương trình toán sẽ đơn giản hơn rất nhiều.

Các công thức lượng giác có rất nhiều cách học dễ nhớ. Mỗi người sẽ có một cách ghi nhớ riêng. Có thể là ghi nhớ một công thức bất kỳ và suy luận ra công thức khác giúp quá trình ghi nhớ dễ dàng hơn. Tuy nhiên thực tế mà nói thì công thức lượng giác dễ học nhưng cũng chóng quên, nếu chỉ học thuộc lòng mà không áp dụng vào các bài toán thì sẽ nhanh chóng quên ngay. Hãy cố gắng học tập và thực hành đi đôi với nhau nhé!

Leave a Reply

Your email address will not be published. Required fields are marked *